One- vs. two-tailed inference¶
Note
This discussion is applicable only to one- and two-sample tests involving the t statistic including t tests and regression.
It is inapplicable to test statistics whos values are always greater than zero (i.e. F, X2 and T2 statistics).
By default spm1d conducts two-tailed inference for one- and two-sample tests.
To force one-tailed inference use the keyword two_tailed, as in the following example.
Import necessary packages:
>>> import numpy as np
>>> import spm1d
Generate ten smooth, random 1D continua sampled at 100 nodes:
>>> np.random.seed(0)
>>> Y = np.random.randn(10,100) +0.21
>>> Y = spm1d.util.smooth(Y, fwhm=10)
Conduct one-sample t test, with one- then two-tailed inference:
>>> t = spm1d.stats.ttest(Y)
>>> ti_1 = t.inference(alpha=0.05, two_tailed=False) #one-tailed inference
>>> ti_2 = t.inference(alpha=0.05, two_tailed=True) #two-tailed inference
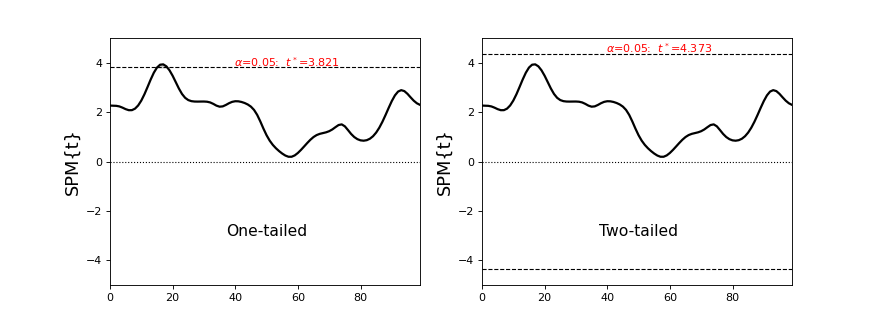
From the results (below) we see that the one-tailed results reach the alpha = 0.05 threshold, and that the two-tailed results do not. The reasons is:
Note
The one-tailed threshold specifies the height that an SPM{t}’s maximum value would reach in only alpha% of many repeated experiments, if those SPM{t}s were generated by smooth, random (Gaussian) continua. The two-tailed threshold contrastingly specifies the height that an SPM{t}’s maximum absolute value would reach in alpha% of many repeated experiments.
In other words, it is more likely that an SPM{t}’s maximum absolute value will reach an arbitrary threshold than its maximum value. Protecting against this increased likelihood, and retaining alpha is fortunately simple:
Note
A one-tailed threshold at alpha is equivalent to a two-tailed threshold at (alpha / 2).
Specifying “two_tailed = True” achieves two goals:
The critical test statistic threshold is set according to (alpha / 2).
Probability values are corrected to the higher threshold, so that an SPM{t} which just touches the threshold will, by definition, yield a p value of alpha.
Warning
Choosing one- vs. two-tailed inference must be done in an a priori manner, before conducting an experiment. If you are unsure which to choose, then you should conduct two-tailed inference. More specifically, if you don’t have a specific hypothesis regarding the direction of a particular effect (e.g. Group A has a greater value than Group B), then it is most objective to expect that the effects could be in either direction.
(Source code, png, hires.png, pdf)