ANOVA¶
Note
p-values for ANOVA
In previous versions of spm1d no p values were generated for ANOVA because they had not yet been validated.
They have now been validated (Pataky, 2015) so now appear in results.
One-way ANOVA¶
./spm1d/examples/stats1d/ex_anova1.py
Method 1 : stacked groups
If data for all groups is stored in a single (J x Q) array and A is a (J x 1) vector containing integers which specify the groups to which each observation belongs, then one-way ANOVA can be conducted like this:
>>> F = spm1d.stats.anova1( Y, A, equal_var=False )
>>> Fi = F.inference(alpha=0.05)
>>> Fi.plot()
Method 2 : separated groups
If there are K groups and data for each group are stored in separate (J_k x Q) variables, where J_k is the number of observations in the Kth group, then one-way ANOVA can be conducted like this:
>>> F = spm1d.stats.anova1( (Y1,Y2,Y3), equal_var=False )
>>> Fi = F.inference(alpha=0.05, interp=True)
>>> Fi.plot()
(Source code, png, hires.png, pdf)
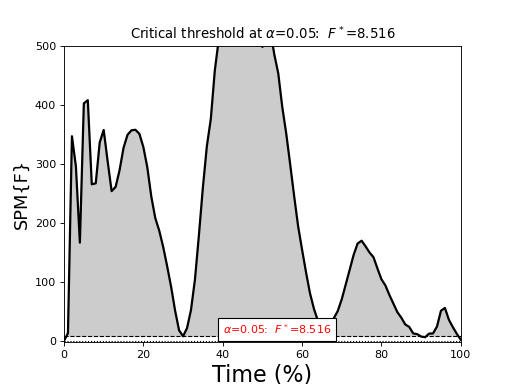
One-way repeated-measures ANOVA¶
./spm1d/examples/stats1d/ex_anova1rm.py
Repeated-measures ANOVA, also called “Within-subjects ANOVA”, can be conducted using Method 1 above and an additional (Jx1) vector of integers which specifies subjects.
>>> F = spm1d.stats.anova1rm( Y, A, SUBJ, equal_var=False )
>>> Fi = F.inference(alpha=0.05)
>>> Fi.plot()
(Source code, png, hires.png, pdf)
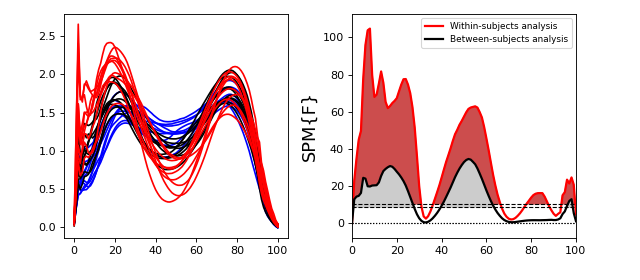
Two-way ANOVA¶
Example:
>>> FF = spm1d.stats.anova2(Y, A, B, equal_var=False)
>>> FFi = [F.inference(alpha=0.05) for F in FF]
>>> FFi[0].plot() #Factor A main effect
>>> FFi[1].plot() #Factor B main effect
>>> FFi[2].plot() #Interaction effect
Two-way nested ANOVA¶
Note
- We do not yet have any real data examples to show.
The factor B is nested inside factor A.
>>> F = spm1d.stats.anova2nested( Y, A, B, equal_var=False )
Two-way repeated-measures ANOVA¶
Note
- We do not yet have any real data examples to show.
Implementing two-way repeated measures ANOVA requires a SUBJ vector:
>>> F = spm1d.stats.anova2rm( Y, A, B, SUBJ )
Danger
Non-sphericity corrections are not yet implemented for this design.
Since non-sphericity corrections weaken results with respect to assumed sphericity, interpret results cautiously, especially when close to alpha.
Two-way ANOVA with repeated-measures on one factor¶
Note
- We do not yet have any real data examples to show.
Implementing two-way repeated measures ANOVA requires a SUBJ vector.
B must be the repeated-measures factor.
>>> F = spm1d.stats.anova2onerm( Y, A, B, SUBJ )
Danger
Non-sphericity corrections are not yet implemented for this design.
Since non-sphericity corrections weaken results with respect to assumed sphericity, interpret results cautiously, especially when close to alpha.
Three-way ANOVA¶
Note
We do not yet have any real data examples to show.
>>> F = spm1d.stats.anova3( Y, A, B, C, equal_var=False )
Three-way nested ANOVA¶
Note
- We do not yet have any real data examples to show.
This is a completely nested design: the factor C is nested inside factor B, which is in turn nested inside factor A.
spm1d currently does not support partial nesting.
>>> F = spm1d.stats.anova3nested( Y, A, B, C, equal_var=False )
Three-way ANOVA with repeated-measures on two factors¶
Note
- We do not yet have any real data examples to show.
Implementing three-way repeated measures ANOVA requires a SUBJ vector.
B and C must be the repeated-measures factor.
>>> F = spm1d.stats.anova3tworm( Y, A, B, C, SUBJ )
Danger
Non-sphericity corrections are not yet implemented for this design.
Since non-sphericity corrections weaken results with respect to assumed sphericity, interpret results cautiously, especially when close to alpha.
Three-way ANOVA with repeated-measures on one factor¶
Note
- We do not yet have any real data examples to show.
Implementing three-way repeated measures ANOVA requires a SUBJ vector.
B and C must be the repeated-measures factor.
>>> F = spm1d.stats.anova3onerm( Y, A, B, C, SUBJ )
Danger
Non-sphericity corrections are not yet implemented for this design.
Since non-sphericity corrections weaken results with respect to assumed sphericity, interpret results cautiously, especially when close to alpha.
