Conjugation analysis

The basic procedure for RFT validations is outlined in Examples/Basic/Validating This section presents code details for validating the probability with which multiple test statistic fields in conjunction will survive particular thresholds.

See ./rft1d/examples/val_conj_1_t.py

Conjunction validations for other test statistic fields are available in scripts titled ./rft1d/examples/val_conj*.py

import numpy as np
from matplotlib import pyplot
import rft1d

#(0) Set parameters:
np.random.seed(0)
nResponses      = 12
nTestStatFields = 2
nNodes          = 101
nIterations     = 2000
FWHM            = 10.0
### derived parameters:
df              = nResponses-1
sqrtN           = np.sqrt(nResponses)
### initialize RFT calculator:
rftcalc         = rft1d.prob.RFTCalculator(STAT='T', df=(1,df), nodes=nNodes, FWHM=FWHM, n=nTestStatFields)

#(1) Generate Gaussian 1D fields, compute test stat:
generator       = rft1d.random.Generator1D(nResponses, nNodes, FWHM)
Tmax            = []
for i in range(nIterations):
        T           = []
        for i in range(nTestStatFields):
                y       = generator.generate_sample()
                t       = y.mean(axis=0) / y.std(ddof=1, axis=0) * sqrtN
                T.append( t )
        Tconj       = np.min(T, axis=0)  #minimum across the test stat fields
        Tmax.append(  Tconj.max()  )
Tmax            = np.array(Tmax)

#(2) Survival functions:
heights     = np.linspace(1, 3, 21)
sf          = np.array(  [ (Tmax>h).mean()  for h in heights]  )
sfE         = rftcalc.sf(heights)  #theoretical

#(3) Plot results:
pyplot.close('all')
ax          = pyplot.axes()
ax.plot(heights, sf,   'o',  label='Simulated')
ax.plot(heights, sfE,  '-',  label='Theoretical')
ax.set_xlabel('$u$', size=20)
ax.set_ylabel('$P(t_\mathrm{conj} > u)$', size=20)
ax.legend()
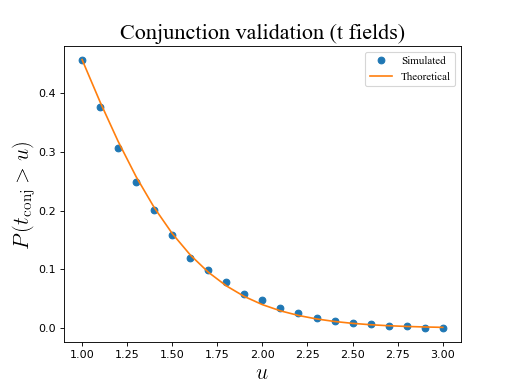
ax.set_title('Conjunction validation (t fields)', size=20)
pyplot.show()

(Source code, png, hires.png, pdf)